This article explains the moment of area or moment of area, application, and example. We will also derive that formula.
First Moment of Area
The first moment of area of a lamina about an axis is defined as the product of the area of the lamina and the perpendicular distance of the center of gravity of the area from the axis.
This moment of area theorem is used to calculate the center of gravity of the area.
We will take a thick lamina or a body having area A.
Let us consider x as the distance of the center of gravity of the area from the axis OY and y as the distance of the center of gravity of the area from the axis OX.
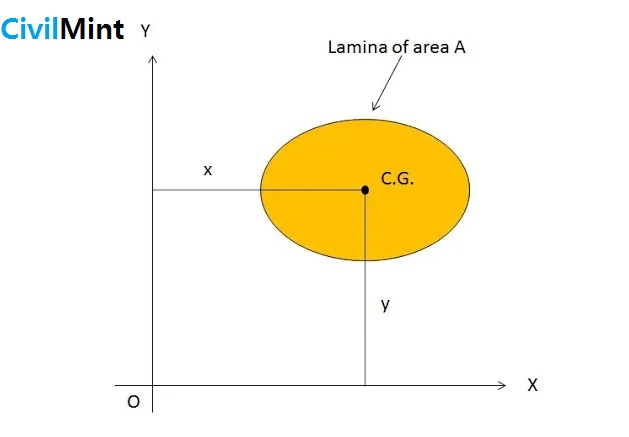
In the above figure,
x = Distance of center of gravity of area A from axis OY
y = Distance of center of gravity of area A from axis OX
Now we will find out the moment of area about axis OY and the moment of area about axis OX.
The moment of area about axis OY = Area * perpendicular distance of the center of gravity of area from the axis OY
The moment of area about axis OY = AX
The above equation is known as the first moment of area about the axis OY.
In the same way,
The moment of area about axis OX= Area * perpendicular distance of the center of gravity of area from the axis OX
The moment of area about axis OX= AY
The above equation is known as the first moment of area about the axis OX.
Let’s take a numerical example to calculate the first moment of area:
If we have a plate with an area of 10 cm2 and the distance from the center of gravity to the axis is expressed as picture below.
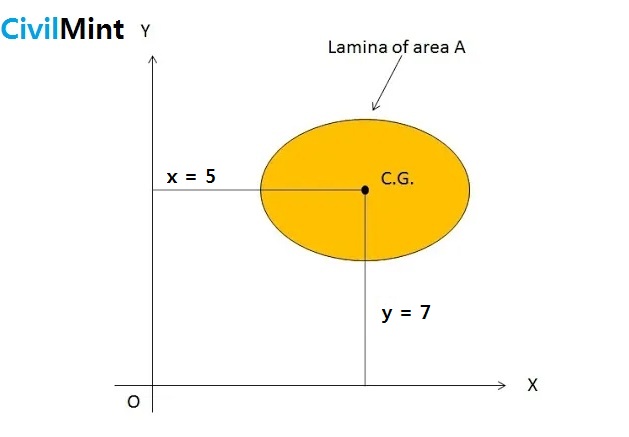
From above figure:
- The first moment of area about axis OY = 10 x 5 = 50
- The first moment of area about axis OX = 10 x 7 = 70
Here we have discussed what the first moment of area is, its formulas, and their applications in numerical problems. If you found this information helpful, please comment below.
