According to Grashof’s law a four-bar linkage framework, the sum of the shortest and longest link of a planar quadrilateral linkage is less than or equal to the sum of the remaining two links, then the shortest link can rotate fully with respect to an adjoining link.
Let us consider a four-bar-linkage system which represents the smallest link by S, the longest link by L, and the & other two links by P and Q.
In case of Grashof’s Law condition is satisfied i.e. S+L ≤ P+Q,
then depending on whether the shortest link ‘S’ is associated with the ground by one end, two ends, or no end there are 3 possible mechanisms.
- Double Crank Mechanism
- Double Rocker mechanism and
- Crank and Rocker Mechanism
Table of Contents
1. Double Crank Mechanism:
In the double crank mechanism, the shortest link ‘S’ is a ground link. Both input crank and output crank rotate at 360 degrees.
Grashof’s condition for the double crank mechanism: s+l > p+ q
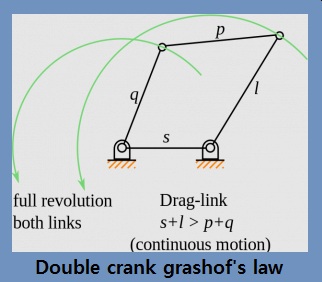
Where,
Let: ‘s’ = length of the shortest link,
‘l’ = length of the longest link,
‘p’ = length of one remaining link and
‘q’ = length of other remaining links.
2. Double Rocker Mechanism:
In the double-rocker mechanism, the shortest link ‘S’ is the coupler link. The coupler link can rotate 360°.
Grashof’s condition for the double crank mechanism: s+l > p+ q
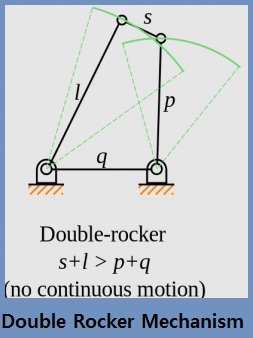
3. Crank and Rocker Mechanism
In the crank and rocker mechanism, the shortest link “S’ is the input crank or output crank. Input crank or output crank rotates 360°.
Grashof’s condition for the double crank mechanism: s+l < p+ q
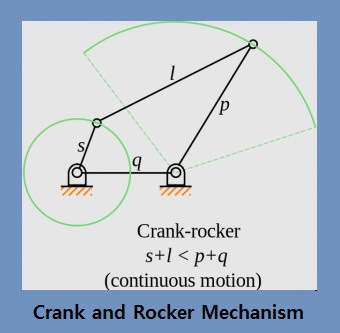
4. Parallel Linkage Mechanism
The parallel linkage mechanism is a very special case of Grashof’s criteria, where the sum of the shortest link ‘S’ & longest link ‘L’ of a planar quadrilateral linkage is less than or equal to the sum of the remaining two links ‘P+Q’.
Grashof’s condition for parallel linkage mechanism: s+l = p+ q
Frequently Asked Questions
1. What is the condition involved in Grashof’s law?
Answer :- s+l≤p+q
As per Grashof’s law, in a four-bar mechanism, the sum of the lengths of the shortest and the longest link should be less than or equal to the sum of the lengths of two remaining links for continuous relative motion between them.
Hence, s+l≤p+q. In the case of Grashof’s law is not truly satisfied, no link will make a complete revolution relative to one another.
2. If the link next to the shortest link is fixed, what type of mechanism is obtained?
Answer:- Crank rocker mechanism
In case the connection next to the shortest link is restricted, the short link is able to rotate continuously and is called a crank. The link inverse to it can only oscillate between limits and is knowns as the rocker. Hence, the mechanism received is the crank rocker mechanism.
Thanks For Reading!
