Table of Contents
Introduction:
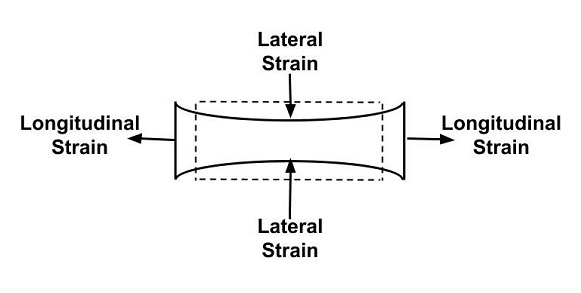
To understand Poisson’s ratio, we have to take an example of a rubber band. Suppose you have a rubber band in perfect cuboidal shape as shown in the figure. Now apply a tensile force on it and start stretching it. Then you will see that the middle portion of the rubber band has been compressed.
The compressed part cross-section area has been reduced because of stretching. Now suppose L and B were the original length and breadth of the rubber band before stretching. Since we have stretched the rubber band its length has increased. So, let’s say dL is the amount by which its length has increased. Similarly, its breadth has been decreased due to stretching. So, assume dB is the amount by which its breath has been reduced.
Poisson’s Ratio Formula
So, Strain developed in the length –
Longitudinal or Axial Strain = ϵ axial = – dL/L
And Strain developed in breadth –
Transverse or Lateral Strain = ϵ trans = – dB/B
From these two equations, we easily find Poisson’s ratio.
Poisson’s Ratio = – ϵt rans/ϵ axial
ϵ trans = Transverse Strain or Lateral Strain
Transverse Strain will be negative for stretching and positive for compressive.
ϵaxial = Longitudinal Strain or Axial Strain
Longitudinal Strain will be positive for extension and negative for compression.
Poisson’s ratio = – ϵtrans/ϵaxial = Transverse Strain/Longitudinal Strain
Where Poisson’s ratio is denoted by ‘nu’.
nu = – ϵtrans/ϵaxial = Transverse Strain/Longitudinal Strain
Since we are taking the ratio of strain which itself is a unitless quantity that’s why Poisson’s ratio also does not have any unit.
Poisson’s ratio values range from – 1.0 to +0.5.
Poisson’s ratio –
From the above formula, we can define Poisson’s ratio as a negative ratio between a transverse or lateral strain of a body to its longitudinal or axial strain.
Poisson Effect
The Poisson’s ratio which we have derived above is actually for measuring the Poisson’s effect on a body. The Poisson effect is a process in which, when we stretch material from one end then it tends to compress itself in the perpendicular direction of the applied force and vice versa. As we have seen in the above example in the case of a rubber band whenever we stretch it, it becomes thinner.
