Table of Contents
Introduction
In this article we will discuss about young’s modulus of elasticity. I would recommend to read my article on stress-strain curve. In the article on stress-strain curves, we learned about proportionality limits, where we talked about constants. This constant is known as the Young’s modulus.
Young’s Modulus of Elasticity
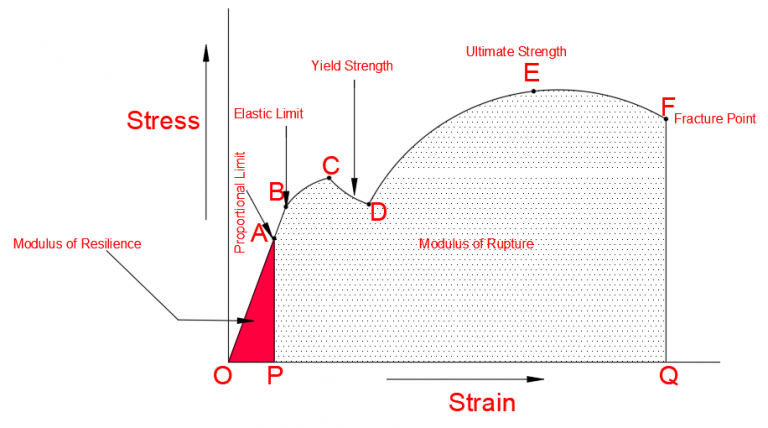
Above graph is obtained by applying increasing loads to a sample of specific dimensions and observing its behavior and dimensional change. Area OA is known as the proportional limit and OB as the elastic limit. Below the elastic limit, stress is directly proportional to strain. This law is known as Hooke’s law. The constant of proportionality for Hooke’s law is known as the young elastic modulus.
By definition;
The ratio of direct stress to longitudinal strain below the yield point is called Young’s modulus. Its units are the same as stress, Newtons per square meter (N/m2). This constant is independent of body dimensions, applied loads, and other boundary conditions, and is unique for each material. It depends only on the type of material and is different for each material.
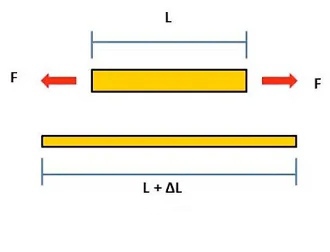
For practical observation, consider a body of length L whose cross-sectional area is equal to A. If a force F acts on a wire and the length change due to load is ΔL
Young’s Modulus of Elasticity Formula in terms of stress and strain is given by;
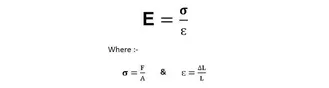
Observation
We have discussed that every unique material have unique value of young modulus. If a material has high value of this constant, it means that this material specimen or object required high value of force to little change in its original dimension. It is less elastic or that material got a little variation in its dimension for a high value of stress. It can say that the high value of modulus shows high rigidity of the material. The value of this modulus for steal is 210 GN/m2.
A small value for this constant for a material means that the material is highly elastic or exhibits very large strains at small stress values. The modulus of elasticity of aluminum is 70 GN/m2.
I also attached Young’s modulus of elasticity table as given below.
| NAME OF MATERIAL | VALUE OF YOUNG MODULUS( GN/m2 ) |
| Plastics | 1 – 3 |
| Aluminum | 70 |
| Brass | 100 – 125 |
| Carbon Fiber | 150 |
| Copper | 120 |
| Glass | 50 – 90 |
| Diamond | 1200 |
| Gold | 75 |
| Gray Cast Iron | 120 – 130 |
| Iron | 210 |
| Stainless Steel | 180 – 190 |
| Tungsten Carbide | 450 – 650 |
| Nylon | 0 – 5 |
Applications
Elastic modulus allows you to calculate the dimensional change under tension or compression of a bar made of isotropic elastic material. For example, predict how much a material sample will expand under tension or shrink under pressure. The modulus of elasticity applies directly in the case of uniaxial stress. i.e. there is tensile or compressive stress in one direction and no stress in the other direction. Young’s modulus is also used to predict the deflection that occurs in a statically determined beam when a load is applied to the points between the beams.
