“Continuity Equation” And Its Assumptions

Let’s assume in the below-shown pipe image an incompressible fluid is going under steady flow.

Now take two points at both ends of the pipe. Let’s say the Left end of the pipe has a cross-section area of A1 and the right end has a cross-section area of A2. In the area, A1 of the pipe assumes the velocity of the fluid is V1 and V2 is the velocity of the fluid in area A2.

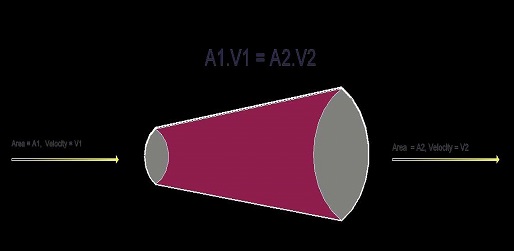
Before we continue towards the “Continuity Equation”. First, we have to understand about “Law Of Conservation Of Mass”. Because from “Law Of Conservation Of Mass” only we are going to derive the “Continuity Equation”.

“Law Of Conservation Of Mass” –

Suppose a bucket or a jar is fully filled with a liquid. Let’s say water in this case. Now, if you add extra water into the fully filled jar then the water will overflow from the jar. The reason behind this is simple. Since the jar was fully filled so it didn’t have space to hold the water which you poured.

Now you have to pay attention to a phenomenon that happened when you poured the extra water into a fully water-filled jar. The amount or volume of water that overflowed due to pouring extra water was equal to the amount or volume of water you poured into the jar.

For better understanding let’s take this example in numerical terms.

For example – Suppose you are pouring 1 liter of extra water into the fully water-filled jar then the amount or volume of water which will overflow will be equal to 1 liter. The amount of overflow water will neither be more nor less. It will be exactly equal to the amount of extra water that you poured into the filled jar.

Since we have understood how the Law Of Conservation Of Mass works. We will return to our original discussion. We already have assumed the cross area and velocity of the fluid.

Now take a small volume of fluid (say x Litre ) from the cross-section area A1 and pushed it to the cross-section area of A2 for a small time called “dt”.

So, according to the law of conservation of mass the amount or volume of fluid lost at area A1 for a small-time “dt”, will be equal to the amounts or volume of fluid gained at the area A2 for the small-time period “dt”.

We already have assumed the velocity of the fluid is V1 at A1 and V2 at A2.

Now, this phenomenon can be written as the: –

⦁ The volume of fluid lost at cross-section area, A1 for small-time “dt” with the fluid velocity V1 = Volume of fluid gained at cross-section area, A2 for small-time “dt” with the fluid velocity V2

⦁ A1. (V1.dt) = A2.(V2.dt)

⦁ A1 = Cross-section area of the left end of the pipe
⦁ A2 = Cross-section area of the right end of the pipe
⦁ V1 = Speed of fluid at cross-section area A1
⦁ V2 = Speed of fluid at cross-section area A2
⦁ dt = It is the small time taken by fluid
⦁ V1. dt = Speed of the fluid at A1 × Time taken by fluid = Distance covered by the fluid at cross-section area of A1.
⦁ V2. dt = Speed of the fluid at A2 × Time taken by fluid = Distance covered by the fluid at cross-section area of A2
⦁ A1. (V1. dt) = Volume of fluid at the left end of the pipe which denoted by A1
⦁ A2. (V2. dt) = Volume of fluid at the right end of the pipe which denoted by A2

Now we got the equation by using the law of conservation of mass: –

⦁ A1. (V1. dt) = A2. (V2. dt)
⦁ A1. V1. dt = A2. V2. dt

Since “dt” is a very small or negligible time. So, we are going to neglect it. It won’t affect our phenomena.

So, now we can write it as: –
⦁ A1. V1= A2. V2

From the above equation, we can conclude that: –

⦁ If an incompressible fluid is flowing under steady flow, then the product of a particular cross-section area in the pipe and the speed of the fluid at that area will be the same for any two random points in the pipe in which the fluid is flowing.

So, we can write the above equation as = AV = Constant

This Is Called “Equation Of Continuity”.

Let’s say, R = Flow rate of the volume of fluid
So, R = AV = Constant,
R = Constant

Assumptions made in the continuity equation

Following are the assumptions made in the “Continuity Equation”: –

⦁ The pipe in which the fluid is flowing is having a single-entry point and a single exit point.
⦁ The fluid flowing is an incompressible fluid.
⦁ The flow of the fluid is steady.
⦁ The viscosity of the fluid is neglected.