This article will tell you how to calculate the length of the roof rafter. But before we get into the calculations, you need to know a few technical terms related to pitched roofs.
The pitched roof is also known as the sloping roof.
What is Rafter Of Roof?
Rafters are the distance between the ridge or hip of the roof and the wall slab of the exterior wall.
What is the Span Of the Roof?
A span is a clear distance between the supports of an arch, beam, or roof truss.
What is the Rise Of Roof?
This is the vertical distance between the wall and the top of the ridges.
What is the Pitch or Slope Of the Roof?
The slope of the roof is the vertical rise above the horizontal span. The angle of the roof is calculated as the number of inches it rises vertically for every 12 inches of horizontal extension. For example, a roof that rises 6 inches for every 12 inches of horizontal purlins has a pitch of 6/12.
There is no standard universal roof slope. It depends on the culture, climate, style, and materials available. The most common roof slopes are 4/12 to 9/12 pitches.
- Pitch = Rise/Run
What is Run Of Roof?
In the roof frame, the run is the distance from the outside of the top wall slab to a point just below the center of the ridge. Simply, the run is a half-distance span.
- Run = Span/2
Exmple 1:

Given,
- Span = 30 ft.
- Pitch = 5/12
Run = Span/2 = 30/2 = 15 ft.
Rafter length =??
According to Pythagoras theorem, a ² + b ² = c ²
Run ² + Rise ² = Rafter ²
Rafter = √ (Run ² + rise ² )
- Pitch = 5/12
- Rise/Run = 5/12
∴ Rise = Run x 5/12 = 15 x 5/12 = 6.25 ft.
Rafter ² = Run ² + Rise ² = 15 ² + 6.25 ² =264.0625
∴ Rafter = √ 264.0625 = 16.25 ft.
Now, let us take another example to bettr know how to calculate length of roof rafter.
Example 2:
Calculate Rafter Length Using Angle:
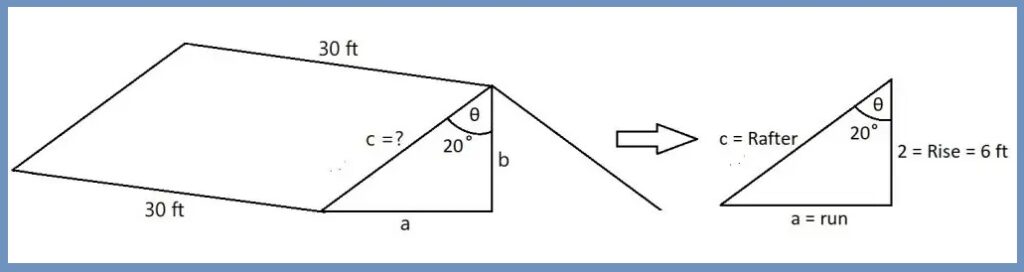
Given,
- Length of roof = 30 ft.
- Rise = 6 ft.
- Angle = 20°
We know,
Sinθ = Opposite/Hypotenuse, Cosθ = Adjacent/Hypotenuse and
tanθ = Opposite/Adjacent
In the above triangle,
- a = Opposite = Run
- b = Adjacent = Rise
- c = Hypotenuse = Rafter
- Cosθ = Adjacent/Hypotenuse = b/c
c = b/Cosθ = 6/Cos20° = 6.38 ft.
∴ Rafter length = 6.38 ft.
I hope you enjoyed my article.
Keep Learning!
