Fourier’s law expresses that “the rate of heat transfer through a material is directly proportional to the negative gradient in the temperature and to the area, at right angles to that slope, through which the heat flows. Fourier’s law, also known as the law of heat conduction.”
The equation of Fourier’s law can be indicated in various forms such as differential form, one-dimensional form, and integral form.
Table of Contents
Differential Form:
q=−k▽T
Where,
- q is the local heat flux density in W.m2
- k is the conductivity of the material in W.m-1.K-1
- ▽T is the temperature gradient in K.m-1
One-Dimensional Form:
qx=−kdTdx
Integral Form:
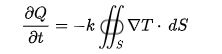
Where,
- ∂Q∂t is the quantity of heat transferred per unit of time
- dS is the surface area
On the basis of differential equation:
Q△t=−kA(△T△x)
Where,
- A is the area of the cross-sectional surface
- ΔT is the temperature difference between the endpoints
- Δx is the distance between two ends
In terms of conductance, we can write above equation as:
△Q△t=UA(−△T)
Where,
- U is the conductance
