Darcy Weisbach Equation Derivation For Head Loss In The Pipe

Introduction Of Darcy Weisbach Equation

Darcy Weisbach Equation is an empirical equation in fluid mechanics named upon Henry Darcy and Julius Weisbach. The Darcy Weisbach Equation associates the loss of pressure or head loss due to friction along the given length of pipe to the average velocity of the fluid flow for an incompressible fluid.

To better understand various types of fluid, I would recommend reading my article on types of fluid.

Darcy Weisbach Equation:

H_F=4fLv²/2gd

Where,

H_F is head loss or pressure loss.

f is the friction coefficient

v is the velocity of incompressible fluid.

L is the length of the pipe.

d is the diameter of the pipe.

g is the acceleration due to gravitational force.

Darcy Weisbach Equation Derivation Derivation:

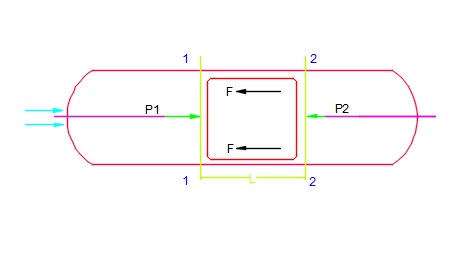
The above figure is a uniform horizontal pipe with a steady flow of fluid.

Assumptions for Uniform Horizontal Pipe with a Steady Flow of Fluid:

1. Consider a uniform horizontal pipe with fixed diameter d and area A, which allow a steady flow of incompressible fluid in the pipe.
2. To make derivation easier consider two sections; S1 and S2 of the pipe separated by the distance L.
3. At all the points of section S1, The pressure is P1, velocity is V1.
4. At all the points of section S2, the pressure is P2 and velocity is V2.
5. Consider the fluid flow as shown in the figure, Hence, the pressure at S1 is more than the pressure at S2 i.e.,(P1>P2) This pressure difference in the pipe makes the fluid flow along the pipe.

As we know When fluid flows there will be a loss of energy due to friction. Hence we can apply Bernoulli’s principle.

Let us apply Berbaulis principle to get our derivation

Bernoulli’s principle:

As per Bernouli’theorm decrease in the pressure or potential energy of the fluid increases the velocity/speed of the fluid flow or in other words, “For an incompressible fluid, the sum of its potential energy, pressure, and velocity remains constant.”

Let us apply Bernoulli’s principle at sections S₁ and S₂

P1+12ρv21+ρgh1=P2+12ρv22+ρgh2+HF —–(1)

Where,

H_F is the head loss due to friction

On dividing above equation (1) by ρg we get equation (2)

P1ρg+v212g+h1=P2ρg+v222g+h2+HF ——-(2)

As we know pipe is horizontal with a uniform cross-section.

The inlet of the pipe and the outlet of the pipe will be at the same level.

Hence, h1=h2.

Due to uniform cross-section.

v1=v2

On substituting into equation (2),

P1ρg+v212g+h1=P2ρg+v212g+h1+HF ⇒P1ρg=P2ρg+HF —–(3)

Hence, on rearranging equation (3) for the head loss we will get equation (4)

HF=P1ρg−P2ρg ⇒HF=P1−P2ρg ⇒HFρg=P1−P2 ——-(4)

The calculation for Frictional Resistance:

Due to the united effect of wet surface and surface roughness of the pipe, the resistance is offered to the flow of fluid because of friction. In consequence, speed is decreased. The Froude was the very first scientist who observe the dependency of frictional resistance with surface roughness.

The frictional resistance cab is expressed using Froude’s formula.

Let us consider f’ be the frictional resistance per unit area(wet) per unit velocity.

so, Frictional resistance F = f’ × wet area × (velocity)2

= f’ × 2＃rL × v2

= f’ ×＃dL × v2

F = f’ × PL × v2 ——-(5)

[here, diameter; d=2r and perimeter; P=＃d]

The net force acting on the fluid at sections S1 and S2

The net force is the sum of Force due to pressure at S1, S2, and Fluid friction.

At section S1, pressure is given by-

P1=F1A

So, The net force F1=P1A

For simplicity of calculation the direction of the force due to pressure as +ve.

At section S2, the pressure is given by-

P2=F2A

Hence, The net force F2=P2A

Let us consider the direction of the force due to pressure as -ve.

Fluid Frictional force(F): It is a resistive force, hence the direction as -ve.

By resolving all the forces along horizontal direction we will get-

P1A – P2A – F = 0

P1A – P2A = F

(P1– P2)A = F

⇒P1−P2=FA ——(6)

Substitute the values for F and (P1– P2) from equations (5) and (4) respectively, we will get

⇒ρgHF=f′PLv2A

By simplifying we will get equation (7)

HF=f′PLv2Aρg HF=f′ρg×Lv2×PA —–(7)

As we know, PA=Wetted perimeter Area=πdπ4d2=4d

Substituting PA=4d in equation(7), we will get equation (8)

(7)⇒HF=f′ρg×4Lv2d ——-(8)

Now we will substitute f′ρ=f2

Where,

f’ is a frictional resistance

⍴ is the density of the fluid.

f is the coefficient of friction

As we consider fluid is incompressible, which means that with the application of the external force there will not be any change in the density.

(8)⇒HF=f2g×4Lv2d

Or

H_F=4fLv²/2gd

Darcy Weisbach’s equation is used to calculate the head loss due to friction in the pipe.

Applications Of Darcy Weisbach Equation

Here are some applications of the Darcy-Weisbach equation:

1. Water Supply Systems:

The Darcy-Weisbach equation can be used to determine the head loss in water supply systems, which is important for designing and sizing pipes, pumps, and other components of the system.

2. HVAC Systems:

In heating, ventilation, and air conditioning (HVAC) systems, the Darcy-Weisbach equation can be used to calculate the pressure drop in ducts and pipes, helping to optimize system performance and energy efficiency.

3. Oil and Gas Pipelines:

The Darcy-Weisbach equation is widely used in the design and operation of oil and gas pipelines, where accurate prediction of pressure drop and flow rates is essential for ensuring safe and efficient transport of petroleum products.

4. Chemical Process Industries:

The Darcy-Weisbach equation is used extensively in chemical process industries to design and optimize pipelines and other fluid handling systems, helping to improve efficiency and reduce costs.

5. Hydraulic Engineering:

In hydraulic engineering applications, the Darcy-Weisbach equation can be used to calculate the head loss in open channels and other complex flow systems, providing critical information for designing and maintaining these systems.

Advantages Of Darcy Weisbach Equation

• The method is grounded in fundamental principles.
• The method maintains dimensional consistency.
• The method is applicable to various types of fluids, such as oil, gas, brine, and sludges.
• The method can be derived analytically for laminar flow.
• The method is useful in the transition region between laminar flow and fully developed turbulent flow.
• The variation of friction factor is well-documented.

Faqs